Sen(Qian)’s Memo

https://proceedings.mlr.press/v97/song19b.html

先行研究の手法は、Loss CorrectionとSample Selectionが主流であるが、それぞれ以下のような欠点がある。

• Loss Correctionでは、遷移行列を特定する(特にclassにのみ依存しインスタンスに依存しないトいう仮定)のは無理ではないか。それによって、false correctionが発生してしまう。
• Sample Selectionでは、信頼できるサンプルのみ選ぶが、難しいサンプルを選ばなくなって結果的にロバストじゃなくなるという欠点を持つ。そして信頼できないサンプルを削除する中で実は信頼できるのに、のようなものを多く消してしまう。

この論文ではSELFIE(Selectively Refurbish Unclean Samples)という手法を開発。Loss CorrectionとSample Selectionの両方のメリットを集めたという。高い精度で正しいラベルに直せる、改修可能なサンプルを、Cleanなサンプルと同時に集めて、back propagationしてパラメタ更新につなげること。高い精度で直せるというのは、モデルがそれなりに正しくないといけないので、ここでもカリキュラム学習を用いて訓練が進むほどその割合を増やす、最終的にはすべてをカバーするようにしている。

既存の手法の性質は以下の通り。

• Flexibility　特定のアーキテクチャに依存しないか
• No Pre-train　事前学習が不要か
• Heavy Noise　高いノイズ率でも性能を残せるか
• Full Exploration　訓練データのすべてを利用するか。

いつも通り自分の読む用のメモみたいな。

この手法はデータを全部利用する上で、高いノイズ率にも頑強である。

$(\mathbf{x}_i, y^*_i)$が真のラベルを持つデータセットで、$D$であるとする。しかし、現実ではラベルがNoisyなデータのバッチ$M$をSGDなどでバッチごとに更新する。$M$に所属するデータは$(\mathbf{x}_i, \bar{y}_i)$であり、ラベルが間違っている可能性がある。

普通ならば、以下のようにSGDで勾配を更新する。

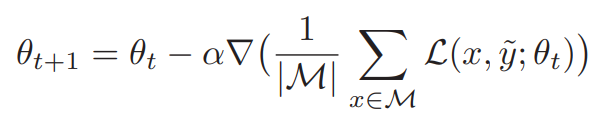
この論文では、$C \subseteq M, R \subseteq M$をまず選ぶ。$C$は完全に正しいラベルを持つデータセットで$R$は修正可能のデータセットである。修正可能とは、back propagationによって、ラベルをもっと正しいと思われるものに修正するということ。つまり、$R$に含まれているラベルは更新によって書き換えられていく。

なお、ここで$C \cap R = \phi$である必要はない。たとえ$C$に入っていたとしても、誤っているかもしれないという考えである。この機構を考えたSGDの勾配更新の式は以下の通り。

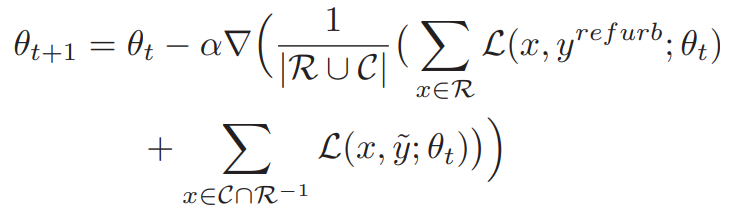
• そもそも$R \cup C$に含まれていないバッチ内のサンプルは、更新に使用しない。
• すべての$R$に含まれているサンプルは、修正後のラベルでlossを計算しback propagationをする。ただし、$|R \cup C|$で割る。
• $C \cap R ^ {-1}$は$C-\{R \cap C\}$に相当する。そこに含まれているものは、正確だということなので、当初のラベルでlossを計算しback propagationする。
• それ以外のものはNoisyであるとして、lossの計算に寄与させない。

この手法の肝心なところは、$C, R$をどのように選ぶかである。

$C$についてはLossが低い順にサンプルを$\tau$の割合で選んでいる。問題はどのように$R$を構築するか。

Noisyなデータに完全に適合する前に、Noisyなラベルに対してのgradientは今までの動きと矛盾した向きへ動くか、今までの通りに一貫するか。

改修可能は明確には以下のように定義されている。$\epsilon \in [0, 1]$とする。

• $\hat{y}_t$はサンプル$\mathbf{x}$の、時刻$t$においての(訓練した)分類器の予測ラベルである。
• $H_x(q)$は、時刻$t=1, \cdots, q$までのサンプル$\mathbf{x}$の予測結果の集合$\{ \hat{y}_t \}_{i=1} ^ q$
• $p(y|x;q)$は、時刻$q$までの予測結果をもとにした、サンプル$\mathbf{x}$がクラス$y$である確率。
  • 単純に、今までの予測したクラス$y$である割合である。
• $\delta$はエントロピーが取りうる最大値。$p(y|x;q)$のエントロピーを$[0,1]$に収めているだけ。
• つまり以下の順番である。
  1. 今まで$q$回の内に$y$を予測した割合を計算する。
  2. それについて、エントロピーを計算する(非常に高いか低い場合は低くなり、ぼんやりだと高く出る)。
  3. それを$\delta$で割って$[0,1]$に収めて正規化する。
  4. その正規化した値が一定値以下の場合、改修可能だとする。つまり、予測結果がほとんど決まっているということだから。

対象のサンプルについて、Noisyなラベル$\bar{y}$を書き換えることがLoss Correctionである。書き換える先は、$\argmax_{1 \leq j \leq K} p(j | x; q)$である。

1. 各タイムステップごとの予測がほぼほぼ決まっているようなものを$R$に入れている。
2. それらに対して、最も所属する可能性が高いクラスを、書き換え後のクラスとしている。
   1. $p(y|x;q)$が高くて$R$に入れられたサンプルは、そのまま新しいラベルは$y$になる。
   2. $p(y|x;q)$が低くて$R$に入れられたサンプルは、ほぼ確実にほかのラベルということなので、これも書き換えていいという扱い。
   3. 定義の通りだと、すでに十分に正しいラベルを持つサンプルも書き換え候補であり、書き換え先と後が同じであっても問題はない。

アルゴリズムの部分で詳しく書くが、各ミニバッチごとに、書き替えした$R$を全体的に蓄積させていく。$R$から消すということはない。

最初には、信頼のおける一部のサンプルだけで学習をさせてから、徐々に学習するサンプルを増やすのが妥当である。

• 最初のWarm-upは普通にNoisyなラベルのままで訓練を行う。Memorization Effectによってそれなりの
  • 学習率は調整してなさそう。SOTAの研究では学習率をわざと大きく学習することで、Noisyな部分を取り込まないようにすることができる。
• Warm-up過ぎたら、先ほど述べたように$R$と$C$のものだけでlossを計算してbackwardする。
• その前に、先ほど述べた方法で$R$を構築する。
• 最終的に全体的に書き換えたサンプルの集合$\mathbb{R}$を返す。次にいうRestartで使うから。
• Restartでは、この訓練が複数回行われることを意味している。
  • 今までの訓練で選び出した$\mathbb{R}$をもとに、もう1回パラメタを初期化して再訓練すること。
  • きれいになったはずの訓練データでもう1回訓練するので、より高い精度を期待できる。

ここにCoteachingの論文を読んで書く。

SELFIEはCoteachingとも組み合わせられる。Coteaching+SELFIEは以下のようなアルゴリズム。

• 2つのネットワークを同時に訓練する。
• 各ミニバッチで、2つのネットはそれぞれCleanな集合、書き換えた後のサンプルの集合を選び出す。
• ネットAはBに自分のCleanな集合、書き換えた後の集合を与えて、それをもとにBのパラメタを更新させる。ネットBも同様にAに与えて更新させる。
• Coteaching自体、訓練サンプルの選択バイアスを消すことに有効であるが、この性質は残ったまま。

Pairwise Noise, Symmetric Noiseの両方において、SELFIEは高ノイズ環境に強いことがわかった！

実データセットにおいてのノイズも、SELFIEは改善している。

Co-teachingについては、Pairwise Noiseではいい性能が出なかった。なぜなら、labelミスされているサンプルのlossはそこまで大きくなかったのが問題。

しかし、同じCo-teachingでも、Symmetric Noiseではちゃんとlabelミスされているサンプルのロスはそれなりに大きかったのでこの手法は有効だった。

Restartによって、訓練に使用したサンプルの数は$\mathbb{R}$の蓄積によって、59.2%から90.2%まで劇的に上昇させた。時間はかかるが、再起動は間違いなく有効である。